▸ Logistic Regression :
Recommended Machine Learning Courses:
- Coursera: Machine Learning
- Coursera: Deep Learning Specialization
- Coursera: Machine Learning with Python
- Coursera: Advanced Machine Learning Specialization
- Udemy: Machine Learning
- LinkedIn: Machine Learning
- Eduonix: Machine Learning
- edX: Machine Learning
- Fast.ai: Introduction to Machine Learning for Coders
- Suppose that you have trained a logistic regression classifier, and it outputs on a new example a prediction
= 0.2. This means (check all that apply):
- Our estimate for P(y = 1|x; θ) is 0.8.
h(x) gives P(y=1|x; θ), not 1 - P(y=1|x; θ)
- Our estimate for P(y = 0|x; θ) is 0.8.
Since we must have P(y=0|x;θ) = 1 - P(y=1|x; θ), the former is
1 - 0.2 = 0.8. - Our estimate for P(y = 1|x; θ) is 0.2.
h(x) is precisely P(y=1|x; θ), so each is 0.2.
- Our estimate for P(y = 0|x; θ) is 0.2.
h(x) is P(y=1|x; θ), not P(y=0|x; θ)
- Our estimate for P(y = 1|x; θ) is 0.8.
- Suppose you have the following training set, and fit a logistic regression classifier
.


Which of the following are true? Check all that apply.- Adding polynomial features (e.g., instead using
) could increase how well we can fit the training data.
- At the optimal value of θ (e.g., found by fminunc), we will have J(θ) ≥ 0.
- Adding polynomial features (e.g., instead using
) would increase J(θ) because we are now summing over more terms.
- If we train gradient descent for enough iterations, for some examples
in the training set it is possible to obtain
.
- Adding polynomial features (e.g., instead using
- For logistic regression, the gradient is given by
. Which of these is a correct gradient descent update for logistic regression with a learning rate of
? Check all that apply.
- Which of the following statements are true? Check all that apply.
- The one-vs-all technique allows you to use logistic regression for problems in which each
comes from a fixed, discrete set of values.
If each
is one of k different values, we can give a label to each
and use one-vs-all as described in the lecture.
- For logistic regression, sometimes gradient descent will converge to a local minimum (and fail to find the global minimum). This is the reason we prefer more advanced optimization algorithms such as fminunc (conjugate gradient/BFGS/L-BFGS/etc).
The cost function for logistic regression is convex, so gradient descent will always converge to the global minimum. We still might use a more advanced optimisation algorithm since they can be faster and don’t require you to select a learning rate.
- The cost function
for logistic regression trained with
examples is always greater than or equal to zero.
The cost for any example
is always
since it is the negative log of a quantity less than one. The cost function
is a summation over the cost for each sample, so the cost function itself must be greater than or equal to zero.
- Since we train one classifier when there are two classes, we train two classifiers when there are three classes (and we do one-vs-all classification).
We will need 3 classfiers. One-for-each class.
- The one-vs-all technique allows you to use logistic regression for problems in which each
Check-out our free tutorials on IOT (Internet of Things):
- Suppose you train a logistic classifier
. Suppose
,
,
. Which of the following figures represents the decision boundary found by your classifier?
- Figure:

In this figure, we transition from negative to positive when x1 goes from left of 6 to right of 6 which is true for the given values of θ.
- Figure:

- Figure:
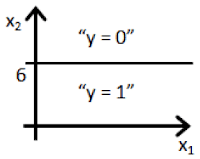
- Figure:

- Figure:
Click here to see solutions for all Machine Learning Coursera Assignments.
&
Click here to see more codes for Raspberry Pi 3 and similar Family.
&
Click here to see more codes for NodeMCU ESP8266 and similar Family.
&
Click here to see more codes for Arduino Mega (ATMega 2560) and similar Family.
Feel free to ask doubts in the comment section. I will try my best to answer it.
If you find this helpful by any mean like, comment and share the post.
This is the simplest way to encourage me to keep doing such work.
&
Click here to see more codes for Raspberry Pi 3 and similar Family.
&
Click here to see more codes for NodeMCU ESP8266 and similar Family.
&
Click here to see more codes for Arduino Mega (ATMega 2560) and similar Family.
Feel free to ask doubts in the comment section. I will try my best to answer it.
If you find this helpful by any mean like, comment and share the post.
This is the simplest way to encourage me to keep doing such work.
Thanks & Regards,
- APDaga DumpBox
- APDaga DumpBox


Fifth question is wrong
ReplyDeleteOk. What do you think the correct answer is??
Deletecorrect answer is D.
DeleteThanks for the response.But simply Not possible.
DeleteIf you substitute to value of theta1 & theta2 in the equation given in the question, you will get x1=6. If you plot the graph x1=6 line, that line will always be parallel to x2 axis.
Correct answer is "A" only.
Please check your question. Only possible reason is your question is slightly different than mine but you didn't read it carefully and copied the answer directly.
Please check once again.
no ur answer is wrong ..it will be D..THANK ME LATER
Deletecan you please provide an explanation supporting to your answer??
DeleteThanks in advance.
Hi @Akshay, your answer is correct. I took the rest, and the reason why shivam and ravi say its D is because the question is different. (I got the same question that they got and the answer is D). The question reverses theta 1 = 0 and theta 2 = 1, in which case D is correct. They read the question wrong
DeleteThank you Sneha.
DeleteThis will help many others.
is there a discord server for discussion?? or asking questions
Delete2nd question has stupid options which dont make much sense without knowing formula
ReplyDeletetheta =
ReplyDelete6
-1
0
y = 1 if 6 + (-1(x1) + (0*x2) => GE(greaterThanEqualTo) 0
6 - x1 => = 0
-x1 => -6
x1 <= (lessThanEqualto) <= 6
therefore the decision boundary is a vertical line where x1=6 and everything to the left
of that denotes y = 1 , while everything to the right denotes y = 0
you don't have to copy somebody's answer it is in the course notes.
Thanks for the detailed explanation.
DeleteSo For other viewers, to avoid the confusion, The correct answer for Que 5 is "A" only.