▸ Neural Networks - Representation :
Recommended Machine Learning Courses:
- Coursera: Machine Learning
- Coursera: Deep Learning Specialization
- Coursera: Machine Learning with Python
- Coursera: Advanced Machine Learning Specialization
- Udemy: Machine Learning
- LinkedIn: Machine Learning
- Eduonix: Machine Learning
- edX: Machine Learning
- Fast.ai: Introduction to Machine Learning for Coders
- Which of the following statements are true? Check all that apply.
- Any logical function over binary-valued (0 or 1) inputs x1 and x2 can be (approximately) represented using some neural network.
- Suppose you have a multi-class classification problem with three classes, trained with a 3 layer network. Let
be the activation of the first output unit, and similarly
and
. Then for any input x, it must be the case that
.
- A two layer (one input layer, one output layer; no hidden layer) neural network can represent the XOR function.
- The activation values of the hidden units in a neural network, with the sigmoid activation function applied at every layer, are always in the range (0, 1).
- Consider the following neural network which takes two binary-valued inputs
and outputs
. Which of the following logical functions does it (approximately) compute?
- AND
This network outputs approximately 1 only when both inputs are 1.
- NAND (meaning “NOT AND”)
- OR
- XOR (exclusive OR)
- AND
- Consider the following neural network which takes two binary-valued inputs
- AND
- NAND (meaning “NOT AND”)
- OR
This network outputs approximately 1 when atleast one input is 1.
- XOR (exclusive OR)
- Consider the neural network given below. Which of the following equations correctly computes the activation
? Note:
is the sigmoid activation
function.
-
Thiscorrectly uses the first row of
and includes the “+1” term of
.
-
-
-
-
- You have the following neural network:
You’d like to compute the activations of the hidden layer. One way to do
so is the following Octave code:
You want to have a vectorized implementation of this (i.e., one that does not use for loops). Which of the following implementations correctly compute ? Check all
that apply.- z = Theta1 * x; a2 = sigmoid (z);
This version computes
correctly in two steps , first the multiplication and then the sigmoid activation.
- a2 = sigmoid (x * Theta1);
- a2 = sigmoid (Theta2 * x);
- z = sigmoid(x); a2 = sigmoid (Theta1 * z);
- z = Theta1 * x; a2 = sigmoid (z);
Check-out our free tutorials on IOT (Internet of Things):
- You are using the neural network pictured below and have learned the parameters
(used to compute
) and
(used to compute
as a function of
and also swap the output layer so
. How will this change the value of the output
- It will stay the same.
Swapping
swaps the hidden layers output
- It will increase.
- It will decrease
- Insufficient information to tell: it may increase or decrease.
- It will stay the same.
Click here to see solutions for all Machine Learning Coursera Assignments.
&
Click here to see more codes for Raspberry Pi 3 and similar Family.
&
Click here to see more codes for NodeMCU ESP8266 and similar Family.
&
Click here to see more codes for Arduino Mega (ATMega 2560) and similar Family.
Feel free to ask doubts in the comment section. I will try my best to answer it.
If you find this helpful by any mean like, comment and share the post.
This is the simplest way to encourage me to keep doing such work.
&
Click here to see more codes for Raspberry Pi 3 and similar Family.
&
Click here to see more codes for NodeMCU ESP8266 and similar Family.
&
Click here to see more codes for Arduino Mega (ATMega 2560) and similar Family.
Feel free to ask doubts in the comment section. I will try my best to answer it.
If you find this helpful by any mean like, comment and share the post.
This is the simplest way to encourage me to keep doing such work.
Thanks & Regards,
- APDaga DumpBox
- APDaga DumpBox
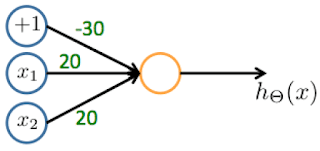
Why I can't represent XOR function without hidden layers? If I have a case like question 2 but with the weights: -10, 20, -20 I would get:
ReplyDeletex1 | x2 | xor
0 | 0 | 0
0 | 1 | 1
1 | 0 | 1
1 | 1 | 0
wouldn't I?
NO.
DeleteIf you consider a NN as given in question 2, with weights as -10, 20, -20 with NN equation -10 + (20*x_1) - (20*x_2) > 0. where threshold for activation is 0.
you will get output as follows:
x1 | x2 | Output | (>0 or not)
0 | 0 | -10 | 0
0 | 1 | -30 | 0
1 | 0 | 10 | 1
1 | 1 | -10 | 1
Which doesn't represent XOR at all.
please explain 2 one some clearly'i did not undertand what is the target of output.
ReplyDeleteI can't understand what exactly you want to ask.
Deletein 2nd question they ask Which of the following logical functions does it (approximately) compute?
ReplyDeleteout put answer what shoud come to satisfy the truth table. In 2 nd one first bit you answered This network outputs approximately 1 only when both inputs are 1.In bit 2 also same.out put howmuch should come to satisfy the truth table.(that means -30,20,10)
Even Though your question is not very clear to me, I am trying to answer it as per my understanding.
Delete1. In Q2(1), Ans is AND gate as Output is 1 when "both" the input are 1.
2. In Q2(2), Ans is OR gate as Output is 1 when "at least one" input is 1.
NOTE: Here we have considered activation threshold = 0.
3. If in Q2, we consider weights as -30, 20, 10 then the ans is AND gate (considering activation threshold = -1)
-30 | 20 | 10
1 | x1 | x2 Output
1 | 0 | 0 = -30 = 0
1 | 0 | 1 = -20 = 0
1 | 1 | 0 = -10 = 0
1 | 1 | 1 = 0 = 1
NOTE: If we consider activation threshold=0 here, then it will be ambiguous for x1=1, x2=1 case. It won't represent AND gate or any other logic gate.
Why question 1 option 2 is incorrect?
ReplyDeleteThe outputs of a neural network are not probabilities, so their sum need not be 1
DeleteTrue. But it represents classes. So exactly one class must be true for a training data. So sum of all the values must be 1. isn't it?
DeleteI didn't get the question numbers 4 and 5 can you please explain in detail?
ReplyDeleteI mean how did writing the vectorized implementation here work in place of for loop? and similarly in question 5 how do I calculate whether output changes or remains same?
consider to the mnn with sigmoidal functions and the training data set x1:0.6,0.2 x2:0.1,0.3 t1:1,0 t2:0,1
ReplyDelete